Dispersión en Variables Cualitativas: Métodos y Cálculo

La dispersión en variables cualitativas es clave para analizar datos. Estas variables se definen como un criterio de clasificación que permite identificar y distinguir un conjunto numerable de categorías nominales o atributos.

Una variable cualitativa es un criterio de clasificación que permite identificar y distinguir un conjunto numerable de categorías nominales o atributos. Se suelen representar por letras latinas mayúsculas (A, B o C) y sus k categorías nominales se pueden denotar con la letra de la variable en minúscula con un subíndice.

Se han definido bastantes medidas de variación para este tipo de variables (Levitt, 2021; Wilcox, 1973); sin embargo, son poco conocidas y utilizadas, aun cuando las variables cualitativas son frecuentes y muy importantes en las ciencias sociales (Maxwell, 2021). De hecho, en la mayoría de los manuales de estadística básica o aplicada no se mencionan y los programas estadísticos comerciales o de acceso libre no las incluyen. Parten de mediados del siglo XX, proliferaron durante las décadas de 1960 y 1970 y continúan siendo desarrolladas en la actualidad (Evren & Erhan, 2017; Li, Garg, & Deng, 2020; Moral, 2022; Weiss, 2019).

En este artículo, se contemplan seis medidas: razón de variación de Freeman (RVF, 1965), razón de variación de Wilcox (RVW, 1973), razón de variación universal (RVU) de Moral (2022), desviación estándar desde la moda (DEM) de Kvalseth (1988), índice de variación cualitativa (IVC) de Gibbs y Poston (1975) y entropía relativa (ERel) de Shannon (1948). Las medidas seleccionadas son de cálculo sencillo, prácticas para su uso, probadas en investigación social y de interpretación clara (Deacon & Stanyer, 2021; Evren, Tuna, Ustaoglu, & Sahin, 2021; Moral, 2022).

DIPLOMADO

ESCRITURA DE ARTÍCULOS CIENTÍFICOS

Desarrolla habilidades para redactar y publicar artículos científicos de alto impacto. Aprende técnicas avanzadas de escritura, normas editoriales y gestión del proceso de publicación. 100 % En Línea.

> Inscríbete Ahora

Un rango de 0 a 1 y su interpretación son características que comparten todas ellas. En este rango, el 0 corresponde a la distribución de una variable aleatoria constante, en la que un valor concentra toda la probabilidad a nivel poblacional o toda la frecuencia a nivel muestral. El valor de 1 corresponde a una distribución uniforme, en la que todos sus valores tienen la misma probabilidad a nivel poblacional o la misma frecuencia a nivel muestral.

Los objetivos de este artículo son presentar las seis medidas de variación y posibilitar su estimación puntual y por intervalo a través de un guion de instrucciones para el programa R, que es de acceso gratuito (R Core Team, 2024a) y de gran utilidad para la investigación en psicología (Barrett, 2019; Miller & Ulrich, 2022). Dicho guion se aplica a un ejemplo.

Razón de variación de Freeman

Fue desarrollada por Freeman (1965) para distribuciones unimodales y se puede denotar con RVF. Parte de una fórmula de variación en torno a la moda y su expresión se simplifica al complemento de la frecuencia de la moda única. Véase la Ecuación 1, donde n_i denota la frecuencia absoluta de cada valor, siendo k el número de valores o categorías cualitativas; n_mo representa la frecuencia absoluta de la moda única (mo); n es el tamaño muestral; f_i simboliza la frecuencia relativa de cada valor; y f_mo constituye la frecuencia relativa de la moda única.

$$ RVF = \frac{\sum_{i=1}^k \left( n_i – \frac{n_{mo}}{k} \right)}{\sum_{i=1}^k n_i} = \frac{\sum_{i=1}^k \left( n_i – \frac{n_{mo}}{k} \right)}{n} = $$ $$ \sum_{i=1}^k \left( \frac{n_i}{n} – \frac{n_{mo}}{k \times n} \right) = \sum_{i=1}^k \left( f_i – \frac{f_{mo}}{k} \right) = $$ $$ \sum_{i=1}^k f_i – \sum_{i=1}^k \frac{f_{mo}}{k} = 1 – \frac{k \times f_{mo}}{k} = 1 – f_{mo} $$

(1)

Razón de variación de Wilcox

Wilcox (1973) publicó una razón de variación estandarizada basada en la moda. Frente a RVF, incluye el número de categorías nominales, a parte de la frecuencia de la moda. Se puede denotar por RVW. Véase Ecuación 2.

$$ RVW = 1 – \frac{\sum_{i=1}^k \left( n_{mo} – n_i \right)}{n(k – 1)} = $$ $$ 1 – \frac{\sum_{i=1}^k n_{mo} – \sum_{i=1}^k n_i}{n(k – 1)} = $$ $$ 1 – \frac{kn_{mo} – n}{n(k – 1)} = 1 – \frac{1}{n} \times \frac{kn_{mo} – n}{k – 1} = $$ $$ 1 – \frac{k \frac{n_{mo}}{n} – \frac{n}{n}}{k – 1} = 1 – \frac{k f_{mo} – 1}{k – 1} $$

(2)

Es sencillo establecer la relación entre la razón de Wilcox (1973) y la de Freeman (1965), donde la primera (RVW) siempre es mayor o igual que la segunda (RVF). Véase Ecuación 3.

$$ RVW = 1 – \frac{k f_{mo} – 1}{k – 1} = \frac{k – 1 – k f_{mo} + 1}{k – 1} = $$ $$ \frac{k}{k – 1} (1 – f_{mo}) = \frac{k}{k – 1} RVF $$

(3)

Razón de variación universal de Moral

Fue desarrollada por Moral (2022) planteó una modificación de la fórmula de Freeman (1965). Esta nueva propuesta permite su aplicación en casos de múltiples modas y considera el número de categorías (k), al igual que hace la razón de variación de Wilcox (1973).

El autor denominó a esta estadística modificada como razón de variación universal (RVU), debido a que puede ser aplicada con cualquier tipo de distribución de variable cualitativa. Véase la Ecuación 4, donde k es el número de categorías cualitativas de la variable; c representa el número de valores con frecuencia máxima (el valor de c puede variar de 1 a k); y f_max denota la frecuencia relativa máxima que corresponde a la moda (f_mo), salvo en una distribución uniforme (c = k), la cual se considera que no tiene moda y el valor de sus frecuencias es 1/k.

$$ RVU = \frac{1 – \frac{1}{c} \times f_{max}}{1 – \max\left(\frac{1}{c} \times f_{max}\right)} = \frac{1 – \frac{1}{c} \times f_{max}}{1 – \frac{1}{k^2}} = $$ $$ \frac{1 – \frac{1}{c} \times f_{max}}{\frac{k^2 – 1}{k^2}} = \frac{k^2}{k^2 – 1} \times \left( 1 – \frac{f_{max}}{c} \right) $$

(4)

En el caso de una moda (c = 1), que es la situación en que la fórmula de Freeman (1965) y RVU son comparables, la RVU arroja a un valor mayor o igual que la de Freeman (1965), al igual que ocurre con la estadística RVW (Wilcox, 1973). Véase Ecuación 5.

$$ RVU = \frac{1 – \frac{1}{c} f_{max}}{\frac{k^2 – 1}{k^2}} = \frac{1 – \frac{1}{1} f_{mo}}{\frac{k^2 – 1}{k^2}} = \frac{k^2}{k^2 – 1} (1 – f_{mo}) = $$ $$ \frac{k^2}{k^2 – 1} RVF \geq RVF = 1 – f_{mo} $$

(5)

A su vez, la razón de variación universal (RVU) es menor o igual que la razón de variación de Wilcox (RVW). Consecuentemente, RVF siempre toma un valor menor o igual que RVU y RVU siempre toma un valor menor o igual que RVW. Véase Ecuación 6.

$$ RVF = \left( 1 – \frac{1}{k^2} \right) \times RVU = \left( 1 – \frac{1}{k} \right) \times RVW $$ $$ \Rightarrow RVF \leq RVU \leq RVW $$

(6)

Desviación estándar desde la moda de Kvalseth

Kvalseth (1988) propuso un nuevo índice estandarizado denominado desviación estándar desde la moda (DEM). Su ventaja es que usa todas las frecuencias. Véase Ecuación 7.

\[ DEM = 1 – \sqrt{\frac{\sum_{i=1}^k \left( f_{mo} – f_i \right)^2}{k – 1}} \]

(7)

Se puede demostrar algebraicamente que el valor de DEM es menor o igual que el índice de Wilcox (1973). Véase Ecuación 8.

$$ DEM = 1 – \sqrt{\frac{\sum_{i=1}^k \left( f_{mo} – f_i \right)^2}{k – 1}} \leq VRW = 1 – \frac{k f_{mo} – 1}{k – 1} $$

(8)

Según se incrementa el tamaño muestral (n → ∞), la distribución del estimador o estadística DEM converge a una distribución normal, por lo que Kvalseth (1988) derivó su error estándar asintótico (EEA), usando el método delta. En la Ecuación 9, se muestra dicho error.

$$ EEA_{DEM} = \sqrt{ \frac{ f_{mo} (1 – k f_{mo})^2 + \sum_{i=1}^k f_i (f_{mo} – f_i)^2 }{ n (k – 1)^2 (1 – DEM)^2 } – \frac{(1 – DEM)^2}{n} } $$

(9)

Cuando el tamaño muestral es grande, no menor de 30, el error estándar asintótico permite hacer estimaciones por intervalo de DEM, como puede verse en la Ecuación 10, donde z_1-α/2 denota el cuantil de orden 1 – α / 2 en una distribución normal estándar, 1 – α es el nivel de confianza y la letra griega sigma mayúscula (Σ) representa la desviación estándar desde la moda poblacional.

$$ P\left( DEM – z_{1 – \frac{\alpha}{2}} \times EEA_{DEM} \leq \Sigma \leq DEM + z_{1 – \frac{\alpha}{2}} \times EEA_{DEM} \right) = 1 – \alpha $$

(10)

Índice de variación cualitativa de Gibbs y Poston

Gibbs y Poston (1975) propusieron la medida de variación cualitativa más empleada, sobre todo en ciencias sociales (Kvalseth, 1988), que también usa todas las frecuencias como DEM (Ecuación 11).

$$ IVC = \frac{k \times \left( 1 – \sum_{i=1}^k f_{x_i}^2 \right)}{k – 1} $$

(11)

Entropía relativa de Shannon

El origen del concepto de entropía procede de la termodinámica, fue aplicado a la teoría de la información por Shannon (1948) y de ahí pasó a la estadística como una propiedad para caracterizar distribuciones tanto discretas como continuas y medir la variabilidad en variables cualitativas. A nivel poblacional se denota con la letra griega mayúscula eta (Η) y a nivel muestral con la letra latina mayúscula E. La entropía es la esperanza matemática de la información de Shannon (1948) o logaritmo de la función de masa de probabilidad.

Para una distribución empírica o muestral, la entropía se calcula con la Ecuación 12, donde f_n(a_i) representa la frecuencia relativa de la categoría a_i de la variable cualitativa A, n_{a_i} denota la frecuencia absoluta de la categoría a_i de la variable A, y n es el tamaño de la muestra.

$$ E = – \sum_{i=1}^k f_n(a_i) \ln(f_n(a_i)) = – \sum_{i=1}^k \frac{n_{a_i}}{n} \ln\left(\frac{n_{a_i}}{n}\right) $$

(12)

Al conocerse el valor máximo de la entropía en una distribución discreta, que corresponde a la distribución uniforme U{a, b}, se puede calcular la entropía normalizada o relativa de Shannon. Este máximo es el logaritmo natural del número de valores (k) en el intervalo acotado de a (mínimo) a b (máximo) del soporte de una distribución uniforme discreta: ln(k), donde k = #{a, b}.

La entropía relativa se denota con Ηrel a nivel poblacional y ERel a nivel muestral, y es la entropía o información promedio dividida por su valor máximo (Shannon, 1948). Para una distribución de frecuencias empíricas o muestrales, la entropía relativa se calcula con la Ecuación 13. En el caso de una variable aleatoria constante, se da un valor de 2 al número de categorías (k).

$$ ERel = \frac{E}{\max(E)} = \frac{- \sum_{i=1}^k f_n(a_i) \ln(f_n(a_i))}{\ln(k)} = $$ $$ \frac{-1 \sum_{i=1}^k \frac{n_{x_i}}{n} \ln\left(\frac{n_{x_i}}{n}\right)}{\ln(k)} $$

(13)

Método

Para obtener la estimación puntual de las seis estadísticas de variación, se aplican las fórmulas previamente vistas con el lenguaje de programación de R (R Core Team, 2024a). Para computar los intervalos de confianza se opta por el método de muestreo repetitivo con reposición, también denominado Bootstrap (Canty, 2022).

Cuando se desconoce la distribución en el muestreo de un estimador o una estadística ( ), se puede acudir a muestreo repetitivo con reposición (Bootstrap) para obtener dicha distribución. A su vez, se puede usar el método de percentil (PERC) para definir el intervalo de confianza.

No obstante, en caso de sesgo (> 0.05) y aceleración (> 0.025), el método de percentil corregido de sesgo y acelerado (PCSA) es mejor opción (Zelikman, Wu, Mu, & Goodman, 2022). Se recomienda generar 1000 muestras (B = 1000). Al calcular la estadística en cada una de las 1000 muestras ( ), se obtiene la distribución en el muestreo Bootstrap del estimador o estadística. El sesgo mide si dicha distribución está centrada en el valor muestral y la aceleración mide la tasa de cambio en la desviación estándar de las estimaciones según cambian las puntuaciones en las muestras generadas (Canty, 2022).

La media de la distribución en el muestreo Bootstrap de la estadística es la estimación puntual Bootstrap, su desviación estándar muestral es el error Bootstrap y la diferencia entre la estimación Bootstrap y la estimación en la muestra original es el sesgo Bootstrap. El cuantil α /2 de dicha distribución constituye el límite inferior y el cuantil de orden 1 – α/2 representa el límite superior del intervalo de confianza por el método PERC.

Para obtener el intervalo por el método PCSA, primero se calcula la corrección de sesgo (z₀^*). Véase Ecuación 14, donde Φ^-1 denota la función probit y I es la función indicatriz.

Se prosigue computando la aceleración (a) desde la distribución en el muestreo Jackknife, que se obtiene al generar n muestras a partir de la original, eliminando un elemento y calculando la estadística en cada una de ellas con sus n – 1 datos ( ). Véase Ecuación 15.

A continuación, se obtienen los órdenes inferior y superior (p_LI y p_LS) del intervalo PCSA. Véase Ecuación 16, donde Φ representa la función de distribución acumulativa normal estándar, z_α/2 es el cuantil de orden α/2 y z₁–_α/2 es el cuantil de orden 1-α/2 de una distribución normal estándar. Los cuantiles en la distribución en el muestreo Bootstrap de la estadística que corresponden a dichos órdenes (p_LI y p_LS) constituyen los límites del intervalo de confianza PCSA (Efron & Narasimhan, 2022).

$$ z_0^* = \Phi^{-1} \left( \frac{\sum_{i=1}^B I\left(\hat{\theta}_i^* \leq \hat{\theta}\right)}{B} \right) $$

(14)

$$ a = \frac{\sum_{i=1}^n \left( \left( \frac{\sum_{i=1}^n \hat{\theta}_{(-i)}}{n} – \hat{\theta}_{(-i)} \right)^3 \right)}{ 6 \left[ \sum_{i=1}^n \left( \frac{\sum_{i=1}^n \hat{\theta}_{(-i)}}{n} – \hat{\theta}_{(-i)} \right)^2 \right]^{3/2}} = $$ $$ \frac{\sum_{i=1}^n \left( \hat{\theta}_{Jackknife} – \hat{\theta}_{(-i)} \right)^3}{ 6 \left[ \sum_{i=1}^n \left( \hat{\theta}_{Jackknife} – \hat{\theta}_{(-i)} \right)^2 \right]^{3/2}} $$

(15)

$$ p_{LI} = \Phi \left( z_0^* + \frac{z_0^* + z_{\alpha/2}}{1 – a\left(z_0^* + z_{\alpha/2}\right)} \right) \quad \text{y} \quad p_{LS} = $$ $$ \Phi \left( z_0^* + \frac{z_0^* + z_{1-\alpha/2}}{1 – a\left(z_0^* + z_{1-\alpha/2}\right)} \right) $$

(16)

Cuando la corrección de sesgo z₀^* presenta un valor extremo, no se puede calcular el intervalo de confianza por el método PCSA, ya que resulta indeterminado. En este caso, se puede dar un valor de 0 a z₀*, lo que arroja un resultado equivalente al método percentil, como sugiere Efron y Narasimhan (2020).

Resultados

En el Apéndice B, se presenta un guion de instrucciones para el programa R que permite calcular las seis medidas de variación previamente presentadas. Para facilitar su identificación, se sintetizan mediante un Cuadro en el Apéndice A. Se aplica a un ejemplo sobre el motivo de elección de carrera.

Para adaptar el guion a otros datos muestrales distintos deben cambiarse los códigos destacados en azul. Estos cambios afectan al primer apartado de “Definición de datos”, el nombre de la tabla (motivo <- names(…) y la instrucción “cat” del apartado de “Tabla de frecuencias”, además de ajustarse el número de categorías en la instrucción “levels = 1:10”, que aparece varias veces en el guion, al igual que el nombre de la tabla. Si son ocho categorías, “levels” pasaría a ser 1:8. También se destacan en azul otros aspectos modificables, como son el nivel de confianza de los intervalos y el número de decimales en los resultados.

El guion desarrollado se puede ejecutar con el programa R y la biblioteca “ggplot2” descargados en la computadora, lo que permite guardar los histogramas como gráficas de alta resolución. Actualmente, la última versión de R es la 4.4.1, la cual se lanzó el 14 de junio de 2024 (R Core Team, 2024a).

Como único requisito adicional, el guion utiliza la librería “ggplot2” (Wickham, 2016). Este paquete fue creado por el estadístico neozelandés Hadley A. Wickham y el ingeniero en cómputo estadounidense Winston Chang. Se lanzó por primera vez el 10 de junio de 2007 y, actualmente, está disponible su versión 3.5.1, liberada el 23 de abril de 2024 (Wikipedia contributors, 2024, 22 de mayo).

El guion puede ejecutarse directamente en R o mediante la consola del entorno de desarrollo integrado RStudio (RStudio Team, 2024). Otra opción es ejecutarlo en línea a través de Snippets (R Core Team, 2024b). En este último caso, se pueden copiar los histogramas mediante una captura de imagen (Alt + Windows + S), aunque se pegarían como gráficas de baja resolución.

En la muestra generada para el ejemplo, que es de tamaño medio (n = 122), la moda es única, por lo que se pueden usar las seis medidas de variación presentadas y el intervalo de confianza asintótico para DEM (Kvalseth, 1988). En caso de dos o más modas, deben omitirse las instrucciones para la razón de variación de Freeman (RVF, 1965) y la razón de variación de Wilcox (RVW, 1967), porque no se pueden calcular. También debe excluirse el cómputo del error estándar y el intervalo de confianza asintóticos de DEM, ya que se basan en un supuesto de unimodalidad, aparte de requerirse una muestra grande (n > 30).

Para dar un significado más concreto en el campo de la psicología al ejemplo generado, se pueden considerar que sus datos corresponden a una muestra aleatoria de 122 estudiantes (99 mujeres y 23 hombres) de una población de 573 estudiantes de psicología de primer semestre de una universidad pública del noreste de México, colectada en agosto de 2023. En dicha muestra, se preguntó por el motivo principal de elección de carrera. Las respuestas a la pregunta abierta se clasificaron en diez categorías nominales (Collisson, Eck, & Harig, 2023).

El guion está desarrollado para los siguientes objetivos analíticos:

Representar la distribución por medio de una tabla de frecuencias.
Calcular la moda como medida de tendencia central.
Computar la razón de variación de Freeman (RVF, 1965), la razón de variación de Wilcox (RVW, 1973), la razón de variación universal (RVU) de Moral (2022), la desviación estándar desde la moda (DEM) de Kvalseth (1988) con su error estándar asintótico, el Índice de Variación Cualitativa (IVC) de Gibbs y Poston (1975) y la entropía relativa (ERel) de Shannon (1948) como medidas de variabilidad.
Estimar por intervalo con un nivel de confianza del 95% las medidas de variación mediante muestreo repetitivo con reposición (Bootstrap) por los métodos percentil (PERC) y percentil corregido de sesgo y acelerado (PCSA).
Obtener el sesgo y error estándar en las estimaciones por remuestreo (Bootstrap), la aceleración Jackknife y representar la distribución en el muestreo Bootstrap usando un histograma con la curva de densidad superpuesta para elegir entre PERC o PCSA.

La amplitud uniforme y el número de intervalos de clase del histograma se determinan por la regla de Freedman y Diaconis (1981), que no requiere supuestos distribucionales (Contreras-Reyes & Brito, 2022). Los cuantiles se calculan con la regla 8 de R, como recomiendan Hyndman y Fan (1996) desde su estudio de simulación, al arrojar las estimaciones más adecuadas con independencia de la distribución que siguen los datos muestrales. Los resultados se redondean a tres decimales. El cálculo de la densidad en la curva superpuesta al histograma se basa en la función kernel gaussiana y el ancho de banda de Silverman (1986), que son las opciones por defecto que trae el paquete ggplot2 para la estimación de la densidad (Wickham, 2016).

Los resultados del guion con los datos previamente presentados (Apéndice B) se muestran a continuación. Incluyen la distribución de frecuencias (Tabla 1), la moda, las seis estadísticas de variación (Apéndice A) con sus intervalos de confianza Bootstrap por los métodos PERC y PCSA, el error estándar e intervalo de confianza asintóticos de DEM, así como los histogramas de las distribuciones en el muestreo Bootstrap de dichas estadísticas (Figuras 1-6).

Tabla 1
Distribución de frecuencias del motivo principal de elección de la carrera de Psicología

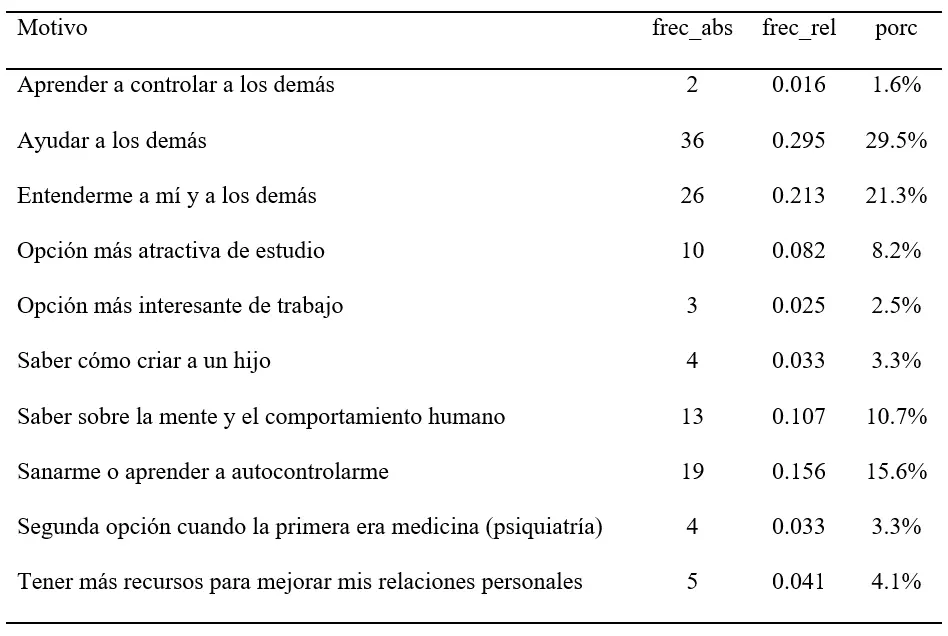
Tamaño de la muestra: n = 122. Número de categorías nominales: k = 10.
Categorías modales: mo = ayudar a los demás.
Número de valores modales: c = 1. Frecuencia relativa de la moda: fmo = 0.295.
Razón de Variación de Freeman (1965): RVF = 0.705.
Estimación Bootstrap de RVF: 0.703.
Sesgo Bootstrap de RVF: -0.002 y Error estándar Bootstrap de RVF: 0.037.
Intervalo de confianza Bootstrap al 95 % por el método percentil para RVF: [0.623, 0.77].
Corrección de sesgo: z_0* = 0.085 y Aceleración Jackknife de RVF: -0.014.
Intervalo de confianza Bootstrap al 95 % por el método PCSA para RVF: [0.631, 0.77].

Figura 1
Distribución en el muestreo Bootstrap de RVF

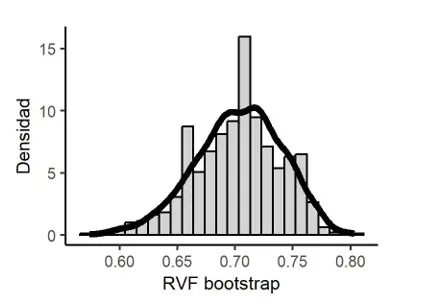
Razón de Variación de Wilcox (1967): RVW = 0.783.
Estimación Bootstrap de RVW: 0.781.
Sesgo Bootstrap de RVW: -0.002 y Error estándar Bootstrap de RVW: 0.042.
Intervalo de confianza Bootstrap al 95% por el método percentil para RVW: [0.692, 0.856].
Corrección de sesgo: z_0* = 0.085 y Aceleración Jackknife de RVW: -0.014.
Intervalo de confianza Bootstrap al 95% por el método PCSA para RVW: 0.701, 0.856].

Figura 2
Distribución en el muestreo Bootstrap de RVW

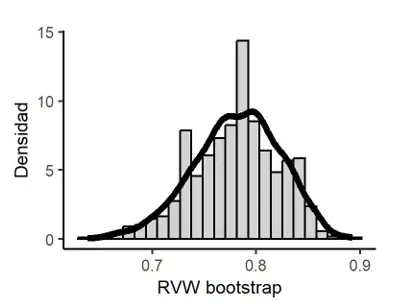
Razón de Variación Universal de Moral (2022): RVU = 0.712.
Estimación Bootstrap de RVU: 0.713.
Sesgo Bootstrap de RVU: 0.001 y Error estándar Bootstrap de RVU: 0.046.
Intervalo de confianza Bootstrap al 95% por el método percentil para RVU: [0.629, 0.841].
Corrección de sesgo: z_0* = 0.083 y Aceleración Jackknife de RVU: -0.014.
Intervalo de confianza Bootstrap al 95% por el método PCSA para RVU: [0.638, 0.878].

Figura 3
Distribución en el muestreo Bootstrap de RVU

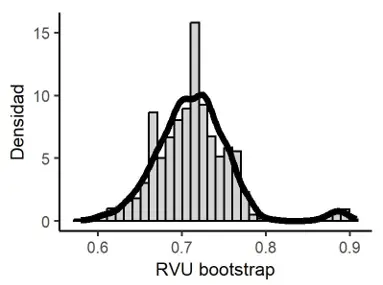
Desviación estándar desde la moda de Tvalseth (1988): DEM = 0.774.
Error estándar asintótico de DEM: EEA(DEM) = 0.043.
Intervalo de confianza asintótico al 95% para DEM: [0.69, 0.858].
Estimación Bootstrap de DEM: 0.771.
Sesgo Bootstrap de DEM: -0.003 y Error estándar Bootstrap de DEM: 0.039.
Intervalo de confianza Bootstrap al 95% por el método percentil para DEM: [0.687, 0.841].
Corrección de sesgo: z_0* = 0.033 y Aceleración Jackknife de DEM: -0.013.
Intervalo de confianza Bootstrap al 95% por el método PCSA para DEM: [0.687, 0.841].

Figura 4
Distribución en el muestreo Bootstrap de DEM

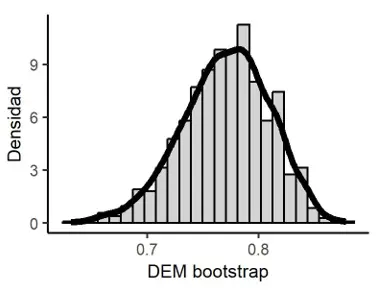
Índice de Variación Cualitativa de Gibbs y Poston (1975): IVC = 0.912.
Estimación Bootstrap de IVC: 0.904.
Sesgo Bootstrap de IVC: -0.008 y Error estándar Bootstrap de IVC: 0.019.
Intervalo de confianza Bootstrap al 95% por el método percentil para IVC: [0.862, 0.94].
Corrección de sesgo: z_0* = 0.335 y Aceleración Jackknife de IVC: 0.002.
Intervalo de confianza Bootstrap al 95% por el método PCSA para IVC: [0.879, 0.948].

Figura 5
Distribución en el muestreo Bootstrap de IVC

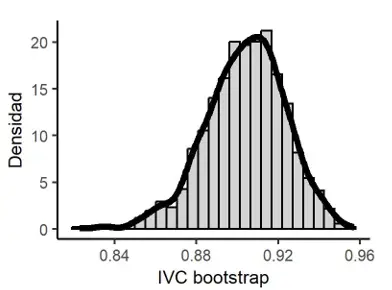
Entropía de Shannon (1948): E = 1.936.
Entropía Relativa de Shannon (1948): ERel = 0.841.
Estimación Bootstrap de ERel: 0.823.
Sesgo Bootstrap de ERel: -0.018 y Error estándar Bootstrap de ERel: 0.032.
Intervalo de confianza Bootstrap al 95% por el método percentil para ERel: [0.759, 0.884].
Corrección de sesgo: z_0* = 0.553 y Aceleración Jackknife de ERel: 0.018.
Intervalo de confianza Bootstrap al 95% por el método PCSA para ERel: [0.798, 0.905].

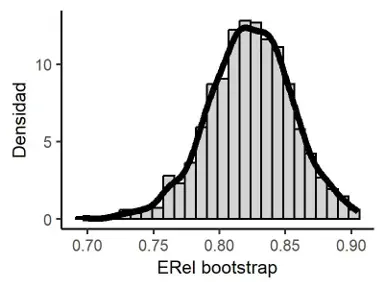
Figura 6
Distribución en el muestreo Bootstrap de ERel

Discusión

Cuando la distribución en el muestreo del estimador o estadística es desconocida o no normal, como es el caso de estas medidas de variación, incluida DEM ante distribuciones bi o multimodales, una mejor opción para obtener el intervalo de confianza, que acudir al método asintótico (intervalo de confianza tipo Wald), es usar un método de muestreo repetitivo no paramétrico o con reposición desde la muestra original (Zelikman et al., 2022). Incluso resulta mejor opción que el método exacto, que suele ser muy conservador (Bertsimas, & Sturt, 2020). No obstante, se recomienda que la muestra sea de al menos 30 datos y se requiere que sea aleatoria para que el procedimiento Bootstrap sea adecuado (Efron & Narasimhan, 2020).

Al aplicar el método Bootstrap usando una muestra con menos de 30 observaciones, pueden surgir varias limitaciones que afectan a la precisión y validez de los intervalos de confianza (Efron & Narasimhan, 2022).

Una primera limitación es la alta dependencia que se tiene de los datos originales al ser estos pocos. El conjunto reducido de datos puede exagerar las características específicas de la muestra original, limitando la capacidad del procedimiento de remuestreo repetitivo para capturar la verdadera variabilidad poblacional; asimismo, puede facilitar el sesgo hacia ciertos valores, incluso atípicos.

Una segunda limitación es obtener una estimación puntual con un acusado sesgo, especialmente cuando se utiliza un muestreo no probabilístico y la variabilidad poblacional es alta, lo que necesariamente se trasladará a las replicaciones Bootstrap. Una tercera limitación es tener una variabilidad alta en las replicaciones debido a la inestabilidad en los datos, generando intervalos de confianza más amplios, esto es, baja eficiencia. Una cuarta limitación es contar con una cobertura insuficiente para hallar el parámetro, aun cuando los intervalos son más amplios para el mismo nivel de confianza (95%) en comparación con muestras de 30 o más datos (Rousselet et al., 2021).

Una muestra aleatoria grande es lo que realmente permite superar estas limitaciones y resulta una mejor solución que aplicar correcciones de sesgo para el estimador o acudir a la probabilidad exacta en caso de que estas opciones existan (Efron & Narasimhan, 2020).

Por lo general, se opta por muestreo con reposición desde la muestra original al desconocerse la distribución en el muestreo del estimador. No obstante, si dicha distribución o una aproximada fuera conocida, se podría usar Bootstrap paramétrico, extrayendo muestras de dicha distribución con el mismo tamaño que la original (n) por el método de transformación inversa. Este método genera las B muestras Bootstrap aplicando la función cuantil de la distribución a B muestras aleatorias uniformemente distribuidas en el intervalo (0, 1) de tamaño n (Groff et al., 2022).

Entre los métodos para obtener el intervalo de confianza Bootstrap destacan los métodos percentil y el percentil corregido de sesgo y acelerado (Rousselet, Pernet, & Wilcox, 2021). Cuando el sesgo y la aceleración Jackknife son pequeños (|sesgo| < 0.1 y |a| < 0.025), ambos métodos son válidos, como se observa en el ejemplo generado. De ahí que los intervalos obtenidos por ambos métodos son muy parecidos.

Sin embargo, cuando estos índices no son pequeños, el método de percentil corregido de sesgo y acelerado es mejor (Efron & Narasimhan, 2020). El mayor problema de este último aparece cuando la corrección de sesgo (z₀^*) alcanza un valor extremo. Para resolver el problema de indefinición, se puede dar a z₀ un valor nulo, como se hace en el guion desarrollado para el programa R. Esto arroja un resultado muy parecido al método percentil, ya que sólo se hace la corrección por aceleración. Cabe señalar que, cuando el sesgo y la aceleración son nulos, los métodos PERC y PCSA coinciden totalmente.

En el guion de instrucciones desarrollado, se usa una semilla para el remuestreo. Este procedimiento se adopta para que la estimación sea estable o reproducible. La elección de la semilla (123) es arbitraria y puede ser cualquier número (Canty, 2022).

La estimación de la aceleración (tasa de cambio en la desviación estándar de las estimaciones según cambian las puntuaciones en las n muestras Jackknife) se realiza por el método Jackknife (de la navaja), siguiendo a Efron y Narasimhan (2022), lo que hace que el resultado sea totalmente estable.

En el método de la navaja, se generan n muestras de tamaño n – 1 a partir de la muestra original de n datos, eliminando un elemento, y en cada una de estas muestras se calcula el estimador. Las n estimaciones obtenidas generan la distribución en el muestreo Jackknife del estimador, donde se calcula la estimación Jackknife (promedio del estimador en dicha distribución) y la aceleración (un sexto de la asimetría de las log-verosimilitudes en la familia exponencial menos favorable que es la distribución en el muestreo Jackknife del estimador).

Se remarca que este guion debe aplicarse con una muestra aleatoria, representativa de la población y con al menos 30 datos, para que la estimación sea válida (Zelikman et al., 2022).

Más allá de las variables de categorías nominales también se puede aplicar complementariamente a variables de categorías ordenadas con un número reducido de órdenes, por ejemplo, estatus social autopercibido (1 = bajo, 2 = medio-bajo, 3 = medio-medio, 4 = medio-alto y 5 = alto) o un ítem tipo Likert (1 = totalmente en desacuerdo, 2 = en desacuerdo, 3 = ni de acuerdo ni en desacuerdo, 4 = de acuerdo y 5 = totalmente de acuerdo).

En caso de 9 o10 categorías ordenadas (por ejemplo, una escala baremada por eneatipos o decatipos) es mejor usar solo medidas de variabilidad propias de variables ordinales, como los rangos, la desviación mediana absoluta, los rangos relativos y el coeficiente de dispersión cuartílico. Incluso con más de 10 categorías ordenadas (por ejemplo, una escala baremada por percentiles) se podrían aplicar medidas de variabilidad propias de variables cuantitativas, como la desviación estándar, la desviación media absoluta y el coeficiente de variación de Pearson (Furr, 2021).

Para aprovechar más la información de la distribución de frecuencias, las medidas de variación para variables en escala de medida nominal más recomendables son: DEM de Kvalseth (1988), IVC de Gibbs y Poston (1975) y ERel de Shannon (1948). De estas tres medidas, DEM muestra menor efecto techo ante la proximidad a la distribución uniforme, que es la distribución limitante para la cota superior de estas estadísticas (Moral, 2022).

Cuando se describen variables cualitativas, se sugiere aplicar estas medidas de variación, facilitado por el presente guion para R, destacando la desviación estándar desde la moda entre todas ellas y la razón de variación universal entre las tres razones de variación (Moral, 2022). Aparte, se invita a usar medidas de la forma (Moral, 2021, 2023), junto con la tabla de frecuencias, las gráficas y la moda como medida de tendencia central. Finalmente, es importante seguir trabajando en el desarrollo y aplicación de medidas descriptivas para estas variables, dado que es un tema escasamente abordado por la estadística (Li et al., 2020).

Conclusiones

Este estudio metodológico presenta seis medidas de dispersión para variables cualitativas y una metodología basada en remuestreo con reposición (Bootstrap) que amplía las herramientas estadísticas disponibles para el análisis de datos categóricos en Psicología. Estas medidas presentan un alto potencial de aplicación en contextos en los cuales se aplican cuestionarios con preguntas abiertas u otras técnicas de investigación cualitativa que requieran análisis de contenido temático para generar variables en una escala de medida nominal, como estudios de representación social, constructos personales, esquemas cognitivos, guiones de vida, contenidos de sueños oníricos y fantasías diurnas, etc. Este enfoque ofrece una forma objetiva de analizar datos cualitativos complejos, complementando las técnicas estadísticas tradicionales.

El script desarrollado para R y estructurado en español, permite calcular las seis estadísticas de dispersión para variables cualitativas expuestas, incluyendo sus intervalos de confianza por los métodos: percentil y percentil corregido de sesgo y acelerado. Solo se requiere como paquete adicional ggplot2 para representar gráficamente las distribuciones en el muestreo Bootstrap de dichas estadísticas.

No obstante, es importante destacar ciertas limitaciones del método, como la dependencia del tamaño muestral y las propiedades del remuestreo que podrían influir en su aplicabilidad en muestras pequeñas. Además, el script presentado, aunque funcional, podría beneficiarse de mejoras como la entrada automática de datos, representación gráfica de la muestra original y la exportación de los análisis en archivos Word o Excel. Estas propuestas representan una vía para el desarrollo futuro del cálculo de medidas descriptivas para variables cualitativas mediante guiones de R y su implementación práctica en el campo de la Psicología.

Barrett, T. S. (2019). Six reasons to consider using R in psychological research. PsyArXiv. https://doi.org/10.31234/osf.io/8mb6d

Bertsimas, D., & Sturt, B. (2020). Computation of exact bootstrap confidence intervals: Complexity and deterministic algorithms. Operations Research, 68(3), 949-964. https://doi.org/10.1287/opre.2019.1904

Canty, A. (2022). Package ‘boot’. https://cran.r-project.org/web/packages/boot/boot.pdf

Collisson, B., Eck, B. E., & Harig, T. (2023). Introducing gen Z psychology majors: Why they choose to major in psychology (and what they expect to learn). Scholarship of Teaching and Learning in Psychology, 9(3), 276-287. https://doi.org/10.1037/stl0000249

Contreras-Reyes, J. E., & Brito, A. (2022). Refined cross-sample entropy based on Freedman-Diaconis rule:‎ application to foreign exchange time series. Journal of Applied and Computational Mechanics, 8(3), 1005-1013. https://doi.org/1005-1013. 10.22055/jacm.2022.39470.3412

Deacon, D., & Stanyer, J. (2021). Media diversity and the analysis of qualitative variation. Communication and the Public, 6, 19-32. https://doi.org/10.1177/20570473211006481

Efron, B. & Narasimhan, B. (2020). The Automatic construction of bootstrap confidence intervals. Journal of Computational and Graphical Statistics, 29(3), 608-619. https://doi.org/10.1080/10618600.2020.1714633

Efron, B. & Narasimhan, B. (2022). Package ‘bcaboot’. Bias corrected bootstrap confidence intervals. https://cran.r-project.org/web/packages/bcaboot/bcaboot.pdf

Evren, A., & Erhan, U. (2017). Measures of qualitative variation in the case of maximum entropy. Entropy, 19(5), article 204, 1-11. https://doi.org/10.3390/e19050204

Evren, A., Tuna, E., Ustaoglu, E., & Sahin, B. (2021). Some dominance indices to determine market concentration, Journal of Applied Statistics, 48(13-15), 2755-2775. https://doi.org/10.1080/02664763.2021.1963421

Freedman, D., & Diaconis, P. (1981). On the histogram as a density estimator: L2 theory. Probability Theory and Related Fields, 57(4), 453–476. https://doi.org/10.1007/BF01025868

Freeman, L. C. (1965). Elementary applied statistics for students in behavioral sciences. New York: John Wiley and Sons. https://doi.org/10.2307/3538646

Furr, R. M. (2021). Psychometrics: an introduction (4th ed.). SAGE publications.

Gibbs, J. P., & Poston, D. L., Jr. (1975). The Division of labor: conceptualization and related measures. Social Forces, 53(3), 468–476. https://doi.org/10.2307/2576589

Golan, A., & Harte, J. (2022). Information theory: A foundation for complexity science. Proceedings of the National Academy of Sciences, 119(33), e2119089119. https://doi.org/10.1073/pnas.2119089119

Goss-Sampson, M. A. (2020). Statistical analysis in JASP: A guide for students (4th ed.). London: University of Greenwich. https://doi.org/10.6084/m9.figshare.9980744

Groff, L. C., Grossman, J. N., Kruve, A., Minucci, J. M., Lowe, C. N., McCord, J. P., Kapraun, D. F., Phillips, K. A., S. Purucker, S. T., Chao, A., Ring, C. L., Williams, A, J. & Sobus, J. R. (2022). Uncertainty estimation strategies for quantitative non-targeted analysis. Analytical and Bioanalytical Chemistry, 414(17), 4919-4933. https://doi.org/10.1007/s00216-022-04118-z

Hyndman, R. J. & Fan, Y. (1996). Sample quantiles in statistical packages. American Statistician, 50(4), 361-365. https://doi.org/10.2307/2684934

Kvalseth, T. O. (1988). Measuring variation for nominal data. Bulletin of the Psychonomic Society, 26(5), 433−436. https://doi.org/10.3758/BF03334906

Levitt, H. M. (2021). Qualitative generalization, not to the population but to the phenomenon: Reconceptualizing variation in qualitative research. Qualitative Psychology, 8(1), 95-110. https://doi.org/10.1037/qup0000184

Li, Y., Garg, H., & Deng, Y. (2020). A new uncertainty measure of discrete Z-numbers. International Journal of Fuzzy Systems, 22, 760-776. https://doi.org/10.1007/s40815-020-00819-8

Maxwell, J. A. (2021). Why qualitative methods are necessary for generalization. Qualitative Psychology, 8(1), 111–118. https://doi.org/10.1037/qup0000173

Miller, J., & Ulrich, R. (2022). Optimizing research output: How can psychological research methods be improved?. Annual Review of Psychology, 73(1), 691-718. https://doi.org/10.1146/annurev-psych-020821-094927

Moral, J. (2021). Una medida de asimetría unidimensional para variables cualitativas. Revista de Psicología, 41(1), 421-459. https://doi.org/10.18800/psico.202201.017

Moral, J. (2022). Una medida de variación para datos cualitativos con cualquier tipo de distribución. Psychologia, 16(2), 63−76. https://doi.org/10.21500/19002386.5642

Moral, J. (2023). Shape measures for the distribution of a qualitative variable. Open Journal of Statistics, 13(4), 619-634. https://doi.org/10.4236/ojs.2023.134030

R Core Team (2024a). R: A language and environment for statistical computing. R Foundation for Statistical Computing. Vienna, Austria. https://www.R-project.org/

R Core Team (2024b). Snippets – Run R code online. Rdrr.io. Disponible en: https://rdrr.io/snippets/

Rousselet, G. A., Pernet, C. R., & Wilcox, R. R. (2021). The percentile bootstrap: a primer with step-by-step instructions in R. Advances in Methods and Practices in Psychological Science, 4(1), https://doi.org/10.1177/2515245920911881

RStudio Team (2024). RStudio: integrated development for R. Boston, MA: RStudio, Inc. Available: http://www.rstudio.com

Shannon, C. E. (1948). A mathematical theory of communication. Bell System Technical Journal, 27(3), 379–423. https://doi.org/10.1002/j.1538-7305.1948.tb01338.x

Silverman, B. W. (1986). Density estimation for statistics and analysis of dada. London: Chapman and Hall. http://dx.doi.org/10.1007/978-1-4899-3324-9

Weiss, C. H. (2019). On the sample coefficient of nominal variation. Springer Proceedings in Mathematics & Statistics, 294, 239-250. https://doi.org/10.1007/978-3-030-28665-1_18

Wickham, H. A. (2016). ggplot2: Elegant Graphics for Data Analysis (2nd ed.). Springer-Verlag. https://ggplot2-book.org/

Wikipedia contributors. (2024, 22 de mayo). ggplot2. En Wikipedia. La enciclopedia libre. Consultado el 6 de noviembre de 2024 en https://en.wikipedia.org/w/index.php?title=Ggplot2&oldid=1225054471

Wilcox, A. R. (1973). Indices of qualitative variation and political measurement. The Western Political Quarterly, 26(2), 325–343. https://doi.org/10.2307/446831

Zelikman, E., Wu, Y., Mu, J., & Goodman, N. (2022). Star: Bootstrapping reasoning with reasoning. Advances in Neural Information Processing Systems, 35, 15476-15488.

APÉNDICES

El Cuadro 1 sintetiza las seis medidas de dispersión presentadas en el artículo e incluidas en el guion para R, indicando su nombre, abreviatura, fórmula y restricción distribucional, considerando una distribución multinomial (variable en escala nominal), aunque también podrían aplicarse a otras distribuciones discretas con un dominio finito (Bernoulli, binomial, hipergeométrica, etc.) y un número limitado de categorías ordenadas (variable en escala ordinal).

Cuadro 1.
Medidas de dispersión para variables medidas en escala nominal

El guion se puede correr en línea desde el sitio web: https://rdrr.io/snippets/ Copie este guion y haga clic en el botón Run. Antes asegúrese que no se haya añadido ningún elemento ajeno al mismo, como el número de páginas, encabezados o pies de página de la revista. A tal fin, se puede pegar el guion en el Bloc de notas de Windows para eliminar posibles caracteres no deseados. Si se utiliza Word u otro procesador de texto para conservarlo como archivo, cerciórese de que el contenido sea solo texto plano y que no se hayan sustituido caracteres, como el símbolo de menos (-) por el guion largo (–).

Una mejor opción es descargar R (https://cran.r-project.org/bin/windows/base/) y el paquete ggplot2 para ejecutarlo en la computadora.

Una vez descargado R, inicie el programa. En la barra de herramientas, vaya al botón de Paquetes y seleccione un espejo de CRAN, desplegando la lista de servidores. Debe escoger el más próximo a su ubicación. Luego, en el mismo botón de Paquetes, haga clic en Instalar paquetes, con lo que se despliega el menú de paquetes ordenados alfabéticamente. Busque ggplot2 y dé clic en dicho paquete. De esta forma, se descarga e instala automáticamente. Otra vía es ejecutar el siguiente comando en la consola de R: install.packages(«ggplot2»), tras haber seleccionado un espejo en CRAN. El comando busca en CRAN e instala automáticamente el paquete ggplot2.

Copie este guion y péguelo en la consola de R. Se ejecutará automáticamente, dando el resultado en la consola y generando seis archivos JPEG en la carpeta de Documentos.

# Datos muestrales y definición de sus etiquetas.

A <- c(«Aprender a controlar a los demás», «Ayudar a los demás», «Entenderme a mí y a los demás», «Opción más atractiva de estudio», «Opción más interesante de trabajo», «Saber cómo criar a un hijo», «Saber sobre la mente y el comportamiento humano», «Sanarme o aprender a autocontrolarme», «Segunda opción cuando la primera era medicina (psiquiatría)», «Tener más recursos para mejorar mis relaciones personales»)

a <- c(3, 4, 8, 3, 2, 3, 7, 4, 2, 2, 2, 7, 7, 2, 2, 2, 6, 3, 4, 8, 3, 7, 2, 9, 6, 2, 2, 8, 7, 2, 3, 10, 3, 3, 4, 2, 3, 3, 3, 7, 5, 8, 7, 4, 2, 5, 2, 7, 5, 3, 8, 8, 7, 4, 3, 2, 2, 7, 2, 10, 2, 2, 8, 9, 3, 3, 4, 7, 2, 2, 1, 3, 3, 3, 3, 6, 2, 2, 9, 2, 8, 10, 3, 2, 8, 2, 3, 2, 8, 2, 2, 3, 8, 3, 8, 4, 8, 3, 6, 3, 7, 1, 2, 10, 8, 8, 2, 3, 4, 9, 2, 8, 2, 4, 8, 2, 10, 8, 7, 8, 2, 2)

# Tabla de frecuencias y nombre de la variable.

tabla_frecuencias <- table(factor(a, levels = 1:10, labels = A))
Motivo <- names(tabla_frecuencias)
frec_abs <- as.vector(tabla_frecuencias)
N <- sum(frec_abs)
fre_rel <- frec_abs / N
frec_rel <- round(frec_abs / N, 3)
porc <- frec_rel * 100
tabla_completa <- data.frame(Motivo, frec_abs, frec_rel, porc)
cat(«Distribución de frecuencias del motivo principal de elección de la carrera de psicología:\n»)
print(tabla_completa)

# Cálculo de la moda muestral.

modas <- Motivo[frec_abs == max(frec_abs)]
frecuencia_moda <- max(fre_rel)
n <- length(a)
k <- length(Motivo)
c <- length(modas)
cat(«Tamaño de la muestra: n =», n, «\n»)
cat(«Número de categorías nominales: k =», k, «\n»)
cat(«Categorías modales: mo =», modas, «\n»)
cat(«Número de valores modales: c =», c, «\n»)
cat(«Frecuencia relativa de la moda: fmo =», round(frecuencia_moda, 3), «\n»)

# Cálculo de la estadística RVF

RVF <- 1 – frecuencia_moda
cat(«Razón de Variación de Freeman (1965): RVF =», round(RVF, 3), «\n»)

# Generación de la distribución en el muestreo de la estadística RVF por remuestreo con reposición desde la muestra original con 1000 extracciones.

set.seed(123)
B <- 1000
RVF_boot <- numeric(B)
for (i in 1:B) {muestra_boot <- sample(a, replace = TRUE)
tabla_frecuencias_boot <- table(factor(muestra_boot, levels = 1:10, labels = A))
frecuencia_moda_boot <- max(tabla_frecuencias_boot) / sum(tabla_frecuencias_boot)
RVF_boot[i] <- 1 – frecuencia_moda_boot
}

# Sesgo y error estándar Bootstrap de RVF

EB_RVF <- mean(RVF_boot)
sesgo_RVF <- mean(RVF_boot) – RVF
ee_RVF <- sd(RVF_boot)
cat(«Estimación Bootstrap de RVF:», round(EB_RVF, 3), «\n»)
cat(«Sesgo Bootstrap de RVF:», round(sesgo_RVF, 3), «\n»)
cat(«Error estándar Bootstrap de RVF:», round(ee_RVF, 3), «\n»)

# Intervalo de confianza Bootstrap al 95% por el método Percentil para RVF

IC_percentil_RVF <- quantile(RVF_boot, c(0.025, 0.975), type = 8)
cat(«Intervalo de confianza Bootstrap al 95% por el método percentil para RVF: [«, round(IC_percentil_RVF[1], 3), «,», round(IC_percentil_RVF[2], 3), «]\n»)

# Corrección de sesgo en el método PCSA

z_0_RVF <- qnorm(sum(RVF_boot <= RVF) / B)
if (is.infinite(z_0_RVF)) {z_0_RVF <- 0} else {z_0_RVF <- z_0_RVF}
cat(«Corrección de sesgo: z_0* =», round(z_0_RVF, 3), «\n»)

# Aceleración por el procedimiento de la navaja (Jackknife) en el método PCSA.

RVF_jackknife <- numeric(n)
for (i in 1:n) {muestra_jackknife <- a[-i]
tabla_frecuencias_jackknife <- table(factor(muestra_jackknife, levels = 1:10, labels = A))
frecuencia_moda_jackknife <- max(tabla_frecuencias_jackknife) / sum(tabla_frecuencias_jackknife)
RVF_jackknife[i] <- 1 – frecuencia_moda_jackknife
}
media_RVF_jackknife <- sum(RVF_jackknife) / n
a_RVF <- sum((media_RVF_jackknife – RVF_jackknife)^3) / (6 * sum((media_RVF_jackknife – RVF_jackknife)^2)^(3/2))
cat(«Aceleración Jackknife de RVF:», round(a_RVF, 3), «\n»)

# Intervalo de confianza Bootstrap al 95% por el método PCSA para RVF

z_LI <- qnorm(0.025)
z_LS <- qnorm(0.975)
LI_PCSA_RVF <- pnorm(z_0_RVF + (z_0_RVF + z_LI) / (1 – a_RVF * (z_0_RVF + z_LI)))
LS_PCSA_RVF <- pnorm(z_0_RVF + (z_0_RVF + z_LS) / (1 – a_RVF * (z_0_RVF + z_LS)))
IC_PCSA_RVF <- quantile(RVF_boot, probs = c(LI_PCSA_RVF, LS_PCSA_RVF), type = 8)
cat(«Intervalo de confianza Bootstrap al 95% por el método PCSA para RVF: [«, round(IC_PCSA_RVF[1], 3), «,», round(IC_PCSA_RVF[2], 3), «]\n»)

# Histograma de densidad de la distribución en el muestreo Bootstrap de la estadística RVF con la curva de densidad superpuesta. La amplitud uniforme y el número de intervalos de clase del histograma se determinan por la regla de Freedman y Diaconis (1981). Las densidades en la curva se estiman mediante la función kernel gaussiana con el ancho de banda establecido por la regla de Silverman (1986).

library(ggplot2)
hist_data1 <- data.frame(RVF_boot)
q25 <- quantile(hist_data1$RVF_boot, 0.25, type = 8)
q75 <- quantile(hist_data1$RVF_boot, 0.75, type = 8)
RIC <- q75 – q25
FD <- 2 * RIC / (length(hist_data1$RVF_boot)^(1/3))
hist_plot1 <- ggplot(hist_data1, aes(x = RVF_boot)) + geom_histogram(binwidth = FD, fill = «lightgrey», color = «black», aes(y = ..density..)) + geom_density(color = «black», size = 1.5) + labs(x = «RVF bootstrap», y = «Densidad») + theme(panel.background = element_rect(fill = «white»), axis.text.x.bottom = element_text(size = 8), axis.text.y = element_text(size = 8), axis.title.x = element_text(size = 9), axis.title.y = element_text(size = 9), axis.line = element_line(color = «black»))
jpeg(«histograma_RVF.jpeg», width = 800, height = 600, units = «px», res = 300)
print(hist_plot1)
dev.off()
hist_plot1

# Cálculo de la estadística RVW

RVW <- k / (k – 1) * (1 – frecuencia_moda)
cat(«Razón de Variación de Wilcox (1967): RVW =», round(RVW, 3), «\n»)

# Generación de la distribución en el muestreo de la estadística RVW por remuestreo con reposición desde la muestra original con 1000 extracciones.

set.seed(123)
B <- 1000
RVW_boot <- numeric(B)
for (i in 1:B) {muestra_boot <- sample(a, replace = TRUE)
tabla_frecuencias_boot <- table(factor(muestra_boot, levels = 1:10, labels = A))
frecuencia_moda_boot <- max(tabla_frecuencias_boot) / sum(tabla_frecuencias_boot)
RVW_boot[i] <- k / (k – 1) * (1 – frecuencia_moda_boot)
}

# Sesgo y error estándar Bootstrap de RVW

EB_RVW <- mean(RVW_boot)
sesgo_RVW <- mean(RVW_boot) – RVW
ee_RVW <- sd(RVW_boot)
cat(«Estimación Bootstrap de RVW:», round(EB_RVW, 3), «\n»)
cat(«Sesgo Bootstrap de RVW:», round(sesgo_RVW, 3), «\n»)
cat(«Error estándar Bootstrap de RVW:», round(ee_RVW, 3), «\n»)

# Intervalo de confianza Bootstrap al 95% por el método Percentil para RVW

IC_percentil_RVW <- quantile(RVW_boot, c(0.025, 0.975), type = 8)
cat(«Intervalo de confianza Bootstrap al 95% por el método percentil para RVW: [«, round(IC_percentil_RVW[1], 3), «,», round(IC_percentil_RVW[2], 3), «]\n»)

# Corrección de sesgo en el método PCSA

z_0_RVW <- qnorm(sum(RVW_boot <= RVW) / B)
if (is.infinite(z_0_RVW)) {z_0_RVW <- 0} else {z_0_RVW <- z_0_RVW}
cat(«Corrección de sesgo: z_0* =», round(z_0_RVW, 3), «\n»)

# Aceleración por el procedimiento de la navaja (Jackknife) en el método PCSA

RVW_jackknife <- numeric(n)
for (i in 1:n) {muestra_jackknife <- a[-i]
tabla_frecuencias_jackknife <- table(factor(muestra_jackknife, levels = 1:10, labels = A))
frecuencia_moda_jackknife <- max(tabla_frecuencias_jackknife) / sum(tabla_frecuencias_jackknife)
RVW_jackknife[i] <- k / (k – 1) * (1 – frecuencia_moda_jackknife)
}
media_RVW_jackknife <- sum(RVW_jackknife) / n
a_RVW <- sum((media_RVW_jackknife – RVW_jackknife)^3) / (6 * sum((media_RVW_jackknife – RVW_jackknife)^2)^(3/2))
cat(«Aceleración Jackknife de RVW:», round(a_RVW, 3), «\n»)

# Intervalo de confianza Bootstrap al 95% por el método PCSA para RVW

LI_CSA_RVW <- pnorm(z_0_RVW + (z_0_RVW + z_LI) / (1-a_RVW*(z_0_RVW+z_LI)))
LS_CSA_RVW <- pnorm(z_0_RVW + (z_0_RVW + z_LS) / (1-a_RVW*(z_0_RVW+z_LS)))
IC_PCSA_RVW <- quantile(RVW_boot, probs = c(LI_CSA_RVW, LS_CSA_RVW), type = 8)
cat(«Intervalo de confianza Bootstrap al 95% por el método PCSA para RVW: [«, round(IC_PCSA_RVW[1], 3), «,», round(IC_PCSA_RVW[2], 3), «]\n»)

# Histograma de densidad de la distribución en el muestreo Bootstrap de la estadística RVW con la curva de densidad superpuesta. La amplitud uniforme y el número de intervalos de clase del histograma se determinan por la regla de Freedman y Diaconis (1981). Las densidades en la curva se estiman mediante la función kernel gaussiana con el ancho de banda establecido por la regla de Silverman (1986).

hist_data2 <- data.frame(RVW_boot)
q25 <- quantile(hist_data2$RVW_boot, 0.25, type = 8)
q75 <- quantile(hist_data2$RVW_boot, 0.75, type = 8)
RIC <- q75 – q25
FD <- 2 * RIC / (length(hist_data2$RVW_boot)^(1/3))
hist_plot2 <- ggplot(hist_data2, aes(x = RVW_boot)) + geom_histogram(binwidth = FD, fill = «lightgrey», color = «black», aes(y = ..density..)) + geom_density(color = «black», size = 1.5) + labs(x = «RVW bootstrap», y = «Densidad») + theme(panel.background = element_rect(fill = «white»), axis.text.x.bottom = element_text(size = 8), axis.text.y = element_text(size = 8), axis.title.x = element_text(size = 9), axis.title.y = element_text(size = 9), axis.line = element_line(color = «black»))
jpeg(«histograma_RVW.jpeg», width = 800, height = 600, units = «px», res = 300)
print(hist_plot2)
dev.off()
hist_plot2

# Cálculo de la estadística RVU

RVU <- k^2 /( k^2-1) * (1 – frecuencia_moda / c)
cat(«Razón de Variación Universal de Moral (2022): RVU =», round(RVU, 3), «\n»)

# Generación de la distribución en el muestreo de la estadística RVU por remuestreo con reposición desde la muestra original con 1000 extracciones

set.seed(123)
B <- 1000
RVU_boot <- numeric(B)
for (i in 1:B) {muestra_boot <- sample(a, replace = TRUE)
tabla_frecuencias_boot <- table(factor(muestra_boot, levels = 1:10, labels = A))
frecuencia_moda_boot <- max(tabla_frecuencias_boot) / sum(tabla_frecuencias_boot)
num_modas_boot <- sum(tabla_frecuencias_boot == max(tabla_frecuencias_boot))
RVU_boot[i] <- k^2 / (k^2 – 1) * (1 – frecuencia_moda_boot / num_modas_boot)
}

# Sesgo y error estándar Bootstrap de RVU

EB_RVU <- mean(RVU_boot)
sesgo_RVU <- mean(RVU_boot) – RVU
ee_RVU <- sd(RVU_boot)
cat(«Estimación Bootstrap de RVU:», round(EB_RVU, 3), «\n»)
cat(«Sesgo Bootstrap de RVU:», round(sesgo_RVU, 3), «\n»)
cat(«Error estándar Bootstrap de RVU:», round(ee_RVU, 3), «\n»)

# Intervalo de confianza Bootstrap al 95% por el método Percentil para RVU

IC_percentil_RVU <- quantile(RVU_boot, c(0.025, 0.975), type = 8)
cat(«Intervalo de confianza Bootstrap al 95% por el método percentil para RVU: [«, round(IC_percentil_RVU[1], 3), «,», round(IC_percentil_RVU[2], 3), «]\n»)

# Corrección de sesgo en el método PCSA

z_0_RVU <- qnorm(sum(RVU_boot <= RVU) / B)
if (is.infinite(z_0_RVU)) {z_0_RVU <- 0} else {z_0_RVU <- z_0_RVU}
cat(«Corrección de sesgo: z_0* =», round(z_0_RVU, 3), «\n»)

# Aceleración por el procedimiento de la navaja (Jackknife) en el método PCSA

RVU_jackknife <- numeric(n)
for (i in 1:n) {muestra_jackknife <- a[-i]
tabla_frecuencias_jackknife <- table(factor(muestra_jackknife, levels = 1:10, labels = A))
frequencia_max_jackknife <- max(tabla_frecuencias_jackknife) /
um(tabla_frecuencias_jackknife)
num_max_frec_max_jackknife <- sum(tabla_frecuencias_jackknife == max(tabla_frecuencias_jackknife))
RVU_jackknife[i] <- k^2 / (k^2 – 1) * (1 – frequencia_max_jackknife / num_max_frec_max_jackknife)
}
media_RVU_jackknife <- sum(RVU_jackknife) / n
a_RVU <- sum((media_RVU_jackknife – RVU_jackknife)^3) / (6 * sum((media_RVU_jackknife – RVU_jackknife)^2)^(3/2))
cat(«Aceleración Jackknife de RVU:», round(a_RVU, 3), «\n»)

# Intervalo de confianza Bootstrap al 95% por el método PCSA para RVU

LI_CSA_RVU <- pnorm(z_0_RVU + (z_0_RVU + z_LI) / (1 – a_RVU * (z_0_RVU + z_LI)))
LS_CSA_RVU <- pnorm(z_0_RVU + (z_0_RVU + z_LS) / (1 – a_RVU * (z_0_RVU + z_LS)))
IC_PCSA_RVU <- quantile(RVU_boot, probs = c(LI_CSA_RVU, LS_CSA_RVU), type = 8)
cat(«Intervalo de confianza Bootstrap al 95% por el método PCSA para RVU: [«, round(IC_PCSA_RVU[1], 3), «,», round(IC_PCSA_RVU[2], 3), «]\n»)

# Histograma de densidad de la distribución en el muestreo Bootstrap de la estadística RVU con la curva de densidad superpuesta. La amplitud uniforme y el número de intervalos de clase del histograma se determinan por la regla de Freedman y Diaconis (1981). Las densidades en la curva se estiman mediante la función kernel gaussiana con el ancho de banda establecido por la regla de Silverman (1986).

hist_data3 <- data.frame(RVU_boot)
q25 <- quantile(hist_data3$RVU_boot, 0.25, type = 8)
q75 <- quantile(hist_data3$RVU_boot, 0.75, type = 8)
RIC <- q75 – q25
FD <- 2 * RIC / (length(hist_data3$RVU_boot)^(1/3))
hist_plot3 <- ggplot(hist_data3, aes(x = RVU_boot)) + geom_histogram(binwidth = FD, fill = «lightgrey», color = «black», aes(y = ..density..)) + geom_density(color = «black», size = 1.5) + labs(x = «RVU bootstrap», y = «Densidad») + theme(panel.background = element_rect(fill = «white»), axis.text.x.bottom = element_text(size = 8), axis.text.y = element_text(size = 8), axis.title.x = element_text(size = 9), axis.title.y = element_text(size = 9), axis.line = element_line(color = «black»))
jpeg(«histograma_RVU.jpeg», width = 800, height = 600, units = «px», res = 300)
print(hist_plot3)
dev.off()
hist_plot3

# Cálculo de la estadística DEM

f_mo <- frecuencia_moda
DEM <- 1 – sqrt(sum((f_mo – fre_rel)^2) / (k – 1))

# Error estándar e intervalo de confianza al 95% asintóticos para DEM

eea <- sqrt((f_mo * (1 – k * f_mo)^2 + sum(fre_rel * (f_mo – fre_rel)^2)) / (N * (k – 1)^2 * (1 – DEM)^2) – (1 – DEM)^2 / N)
alpha <- 0.05
z_crit <- qnorm(1 – alpha / 2)
IC_asintotico_DEM <- c(DEM – z_crit * eea, DEM + z_crit * eea)
cat(«Desviación estándar desde la moda de Tvalseth (1988): DEM =», round(DEM, 3), «\n»)
cat(«Error estándar asintótico de DEM: EEA(DEM) =», round(eea, 3), «\n»)
cat(«Intervalo de confianza asintótico al 95% para DEM: [«, round(IC_asintotico_DEM[1], 3), «,», round(IC_asintotico_DEM[2], 3), «]\n»)

# Generación de la distribución en el muestreo de la estadística DEM por remuestreo con reposición desde la muestra original con 1000 extracciones.

set.seed(123)
B <- 1000
DEM_boot <- numeric(B)
for (i in 1:B) {muestra_boot <- sample(a, replace = TRUE)
tabla_frecuencias_boot <- table(factor(muestra_boot, levels = 1:10, labels = A))
frecuencia_moda_boot <- max(tabla_frecuencias_boot) / sum(tabla_frecuencias_boot)
fre_rel_boot <- as.vector(tabla_frecuencias_boot) / sum(tabla_frecuencias_boot)
DEM_boot[i] <- 1 – sqrt(sum((frecuencia_moda_boot – fre_rel_boot)^2) / (k – 1))
}

# Sesgo y error estándar Bootstrap de DEM

EB_DEM <- mean(DEM_boot)
sesgo_DEM <- mean(DEM_boot) – DEM
ee_DEM <- sd(DEM_boot)
cat(«Estimación Bootstrap de DEM:», round(EB_DEM, 3), «\n»)
cat(«Sesgo Bootstrap de DEM:», round(sesgo_DEM, 3), «\n»)
cat(«Error estándar Bootstrap de DEM:», round(ee_DEM, 3), «\n»)

# Intervalo de confianza Bootstrap al 95% por el método Percentil para DEM

IC_percentil_DEM <- quantile(DEM_boot, c(0.025, 0.975), type = 8)
cat(«Intervalo de confianza Bootstrap al 95% por el método percentil para DEM: [«, round(IC_percentil_DEM[1], 3), «,», round(IC_percentil_DEM[2], 3), «]\n»)

# Corrección de sesgo en el método PCSA

z_0_DEM <- qnorm(sum(DEM_boot <= DEM) / B)
if (is.infinite(z_0_DEM)) {z_0_DEM <- 0} else {z_0_DEM <- z_0_DEM}
cat(«Corrección de sesgo: z_0* =», round(z_0_DEM, 3), «\n»)

# Aceleración por el procedimiento de la navaja (Jackknife) en el método PCSA

DEM_jackknife <- numeric(n)
for (i in 1:n) {muestra_jackknife <- a[-i]
tabla_frecuencias_jackknife <- table(factor(muestra_jackknife, levels = 1:10, labels = A))
frecuencia_moda_jackknife <- max(tabla_frecuencias_jackknife) / sum(tabla_frecuencias_jackknife)
fre_rel_jackknife <- as.vector(tabla_frecuencias_jackknife) / sum(tabla_frecuencias_jackknife)
DEM_jackknife[i] <- 1 – sqrt(sum((frecuencia_moda_jackknife – fre_rel_jackknife)^2) / (k – 1))
}
media_DEM_jackknife <- sum(DEM_jackknife) / n
a_DEM <- sum((media_DEM_jackknife – DEM_jackknife)^3) / (6 * sum((media_DEM_jackknife – DEM_jackknife)^2)^(3/2))
cat(«Aceleración Jackknife de DEM:», round(a_DEM, 3), «\n»)

# Intervalo de confianza Bootstrap al 95% por el método PCSA para DEM

LI_CSA_DEM <- pnorm(z_0_DEM + (z_0_DEM + z_LI) / (1 – a_DEM * (z_0_DEM + z_LI)))
LS_CSA_DEM <- pnorm(z_0_DEM + (z_0_DEM + z_LS) / (1 – a_DEM * (z_0_DEM + z_LS)))
IC_PCSA_DEM <- quantile(DEM_boot, probs = c(LI_CSA_DEM, LS_CSA_DEM), type = 8)
cat(«Intervalo de confianza Bootstrap al 95% por el método PCSA para DEM: [«, round(IC_PCSA_DEM[1], 3), «,», round(IC_PCSA_DEM[2], 3), «]\n»)

# Histograma de densidad de la distribución en el muestreo Bootstrap de la estadística DEM con la curva de densidad superpuesta. La amplitud uniforme y el número de intervalos de clase del histograma se determinan por la regla de Freedman y Diaconis (1981). Las densidades en la curva se estiman mediante la función kernel gaussiana con el ancho de banda establecido por la regla de Silverman (1986).

hist_data4 <- data.frame(DEM_boot)
q25 <- quantile(hist_data4$DEM_boot, 0.25, type = 8)
q75 <- quantile(hist_data4$DEM_boot, 0.75, type = 8)
RIC <- q75 – q25
FD <- 2 * RIC / (length(hist_data4$DEM_boot)^(1/3))
hist_plot4 <- ggplot(hist_data4, aes(x = DEM_boot)) + geom_histogram(binwidth = FD, fill = «lightgrey», color = «black», aes(y = ..density..)) + geom_density(color = «black», size = 1.5) + labs(x = «DEM bootstrap», y = «Densidad») + theme(panel.background = element_rect(fill = «white»), axis.text.x.bottom = element_text(size = 8), axis.text.y = element_text(size = 8), axis.title.x = element_text(size = 9), axis.title.y = element_text(size = 9), axis.line = element_line(color = «black»))
jpeg(«histograma_DEM.jpeg», width = 800, height = 600, units = «px», res = 300)
print(hist_plot4)
dev.off()
hist_plot4

# Cálculo de la estadística IVC

IVC <- k / (k – 1) * (1 – sum(fre_rel^2))
cat(«Índice de Variación Cualitativa de Gibbs y Poston (1975): IVC =», round(IVC, 3), «\n»)

# Generación de la distribución en el muestreo de la estadística IVC por remuestreo con reposición desde la muestra original con 1000 extracciones

set.seed(123)
B <- 1000
IVC_boot <- numeric(B)
for (i in 1:B) {muestra_IVC_boot <- sample(a, replace = TRUE)
tabla_frecuencias_boot <- table(factor(muestra_IVC_boot, levels = 1:10, labels = A))
fre_rel_boot <- as.vector(tabla_frecuencias_boot) / sum(tabla_frecuencias_boot)
IVC_boot[i] <- k / (k – 1) * (1 – sum(fre_rel_boot^2))
}

# Sesgo y error estándar Bootstrap de IVC

EB_IVC <- mean(IVC_boot)
sesgo_IVC <- mean(IVC_boot) – IVC
ee_IVC <- sd(IVC_boot)
cat(«Estimación Bootstrap de IVC:», round(EB_IVC, 3), «\n»)
cat(«Sesgo Bootstrap de IVC:», round(sesgo_IVC, 3), «\n»)
cat(«Error estándar Bootstrap de IVC:», round(ee_IVC, 3), «\n»)

# Intervalo de confianza Bootstrap al 95% por el método Percentil para IVC

IC_percentil_IVC <- quantile(IVC_boot, c(0.025, 0.975), type = 8)
cat(«Intervalo de confianza Bootstrap al 95% por el método percentil para IVC: [«, round(IC_percentil_IVC[1], 3), «,», round(IC_percentil_IVC[2], 3), «]\n»)

# Corrección de sesgo en el método PCSA

z_0_IVC <- qnorm(sum(IVC_boot <= IVC) / B)
if (is.infinite(z_0_IVC)) {z_0_IVC <- 0} else {z_0_IVC <- z_0_IVC}
cat(«Corrección de sesgo: z_0* =», round(z_0_IVC, 3), «\n»)

# Aceleración por el procedimiento de la navaja (Jackknife) en el método PCSA

IVC_jackknife <- numeric(n)
for (i in 1:n) {muestra_jackknife <- a[-i]
tabla_frecuencias_jackknife <- table(factor(muestra_jackknife, levels = 1:10, labels = A))
frecuencia_moda_jackknife <- max(tabla_frecuencias_jackknife) / sum(tabla_frecuencias_jackknife)
fre_rel_jackknife <- as.vector(tabla_frecuencias_jackknife) / sum(tabla_frecuencias_jackknife)
IVC_jackknife [i] <- k / (k – 1) * (1 – sum(fre_rel_jackknife ^2))
}
media_IVC_jackknife <- sum(IVC_jackknife) / n
a_IVC <- sum((media_IVC_jackknife – IVC_jackknife)^3) / (6 * sum((media_IVC_jackknife – IVC_jackknife)^2)^(3/2))
cat(«Aceleración Jackknife de IVC:», round(a_IVC, 3), «\n»)

# Intervalo de confianza Bootstrap al 95% por el método PCSA para IVC

LI_PCSA_IVC <- pnorm(z_0_IVC + (z_0_IVC + z_LI) / (1 – a_IVC * (z_0_IVC + z_LI)))
LS_PCSA_IVC <- pnorm(z_0_IVC + (z_0_IVC + z_LS) / (1 – a_IVC * (z_0_IVC + z_LS)))
IC_PCSA_IVC <- quantile(IVC_boot, probs = c(LI_PCSA_IVC, LS_PCSA_IVC), type = 8)
cat(«Intervalo de confianza Bootstrap al 95% por el método PCSA para IVC: [«, round(IC_PCSA_IVC[1], 3), «,», round(IC_PCSA_IVC[2], 3), «]\n»)

# Histograma de densidad de la distribución en el muestreo Bootstrap de la estadística IVC con la curva de densidad superpuesta. La amplitud uniforme y el número de intervalos de clase del histograma se determinan por la regla de Freedman y Diaconis (1981). Las densidades en la curva se estiman mediante la función kernel gaussiana con el ancho de banda establecido por la regla de Silverman (1986)

hist_data5 <- data.frame(IVC_boot)
q25 <- quantile(hist_data5$IVC_boot, 0.25, type = 8)
q75 <- quantile(hist_data5$IVC_boot, 0.75, type = 8)
RIC <- q75 – q25
FD <- 2 * RIC / (length(hist_data5$IVC_boot)^(1/3))
hist_plot5 <- ggplot(hist_data5, aes(x = IVC_boot)) + geom_histogram(binwidth = FD, fill = «lightgrey», color = «black», aes(y = ..density..)) + geom_density(color = «black», size = 1.5) + labs(x = «IVC bootstrap», y = «Densidad») + theme(panel.background = element_rect(fill = «white»), axis.text.x.bottom = element_text(size = 8), axis.text.y = element_text(size = 8), axis.title.x = element_text(size = 9), axis.title.y = element_text(size = 9), axis.line = element_line(color = «black»))
jpeg(«histograma_IVC.jpeg», width = 800, height = 600, units = «px», res = 300)
print(hist_plot5)
dev.off()
hist_plot5

# Cálculo de la estadística Erel

entropia <- -sum(fre_rel * log(fre_rel + (fre_rel == 0)))
ERel <- entropia / log(k)
cat(«Entropía de Shannon (1948): E =», round(entropia, 3), «\n»)
cat(«Entropía Relativa de Shannon (1948): ERel =», round(ERel, 3), «\n»)

# Generación de la distribución en el muestreo de la estadística ERel por remuestreo con reposición desde la muestra original con 1000 extracciones

set.seed(123)
B <- 1000
ERel_boot <- numeric(B)
for (i in 1:B) {muestra_ERel_boot <- sample(a, replace = TRUE)
tabla_frecuencias_boot <- table(factor(muestra_ERel_boot, levels = 1:10, labels = A))
fre_rel_boot <- as.vector(tabla_frecuencias_boot) / sum(tabla_frecuencias_boot)
entropia_boot <- -sum(fre_rel_boot * log(fre_rel_boot + (fre_rel_boot == 0)))
ERel_boot[i] <- entropia_boot / log(k)
}

# Sesgo y error estándar Bootstrap de IVC

EB_ERel <- mean(ERel_boot)
sesgo_ERel <- mean(ERel_boot) – ERel
ee_ERel <- sd(ERel_boot)
cat(«Estimación Bootstrap de ERel:», round(EB_ERel, 3), «\n»)
cat(«Sesgo Bootstrap de ERel:», round(sesgo_ERel, 3), «\n»)
cat(«Error estándar Bootstrap de ERel:», round(ee_ERel, 3), «\n»)

# Intervalo de confianza Bootstrap al 95% por el método Percentil para ERel

IC_percentil_ERel <- quantile(ERel_boot, c(0.025, 0.975), type = 8)
cat(«Intervalo de confianza Bootstrap al 95% por el método percentil para ERel: [«, round(IC_percentil_ERel[1], 3), «,», round(IC_percentil_ERel[2], 3), «]\n»)

# Corrección de sesgo en el método PCSA

z_0_ERel <- qnorm(sum(ERel_boot <= ERel) / B)
if (is.infinite(z_0_ERel)) {z_0_ERel <- 0} else {z_0_ERel <- z_0_ERel}
cat(«Corrección de sesgo: z_0* =», round(z_0_ERel, 3), «\n»)

# Aceleración por el procedimiento de la navaja (Jackknife) en el método PCSA

ERel_jackknife <- numeric(n)
for (i in 1:n) {muestra_jackknife <- a[-i]
tabla_frecuencias_jackknife <- table(factor(muestra_jackknife, levels = 1:10, labels = A))
fre_rel_jackknife <- as.vector(tabla_frecuencias_jackknife) / sum(tabla_frecuencias_jackknife)
E_jackknife <- -sum(fre_rel_jackknife * log(fre_rel_jackknife + (fre_rel_jackknife == 0)))
ERel_jackknife [i] <- E_jackknife / log(k)
}
media_ERel_jackknife <- sum(ERel_jackknife) / n
a_ERel <- sum((media_ERel_jackknife – ERel_jackknife)^3) / (6 * sum((media_ERel_jackknife – ERel_jackknife)^2)^(3/2))
cat(«Aceleración Jackknife de ERel:», round(a_ERel, 3), «\n»)

# Intervalo de confianza Bootstrap al 95% por el método PCSA para ERel.

LI_PCSA_ERel <- pnorm(z_0_ERel + (z_0_ERel + z_LI) / (1 – a_ERel * (z_0_ERel + z_LI)))
LS_PCSA_ERel <- pnorm(z_0_ERel + (z_0_ERel + z_LS) / (1 – a_ERel * (z_0_ERel + z_LS)))
IC_PCSA_ERel <- quantile(ERel_boot, probs = c(LI_PCSA_ERel, LS_PCSA_ERel), type = 8)
cat(«Intervalo de confianza Bootstrap al 95% por el método PCSA para ERel: [«, round(IC_PCSA_ERel[1], 3), «,», round(IC_PCSA_ERel[2], 3), «]\n»)

# Histograma de densidad de la distribución en el muestreo Bootstrap de la estadística ERel con la curva de densidad superpuesta. La amplitud uniforme y el número de intervalos de clase del histograma se determinan por la regla de Freedman y Diaconis (1981). Las densidades en la curva se estiman mediante la función kernel gaussiana con el ancho de banda establecido por la regla de Silverman (1986)

hist_data6 <- data.frame(ERel_boot)
q25 <- quantile(hist_data6$ERel_boot, 0.25, type = 8)
q75 <- quantile(hist_data6$ERel_boot, 0.75, type = 8)
RIC <- q75 – q25
FD <- 2 * RIC / (length(hist_data6$ERel_boot)^(1/3))
hist_plot6 <- ggplot(hist_data6, aes(x = ERel_boot)) + geom_histogram(binwidth = FD, fill = «lightgrey», color = «black», aes(y = ..density..)) + geom_density(color = «black», size = 1.5) + labs(x = «ERel bootstrap», y = «Densidad») + theme(panel.background = element_rect(fill = «white»), axis.text.x.bottom = element_text(size = 8), axis.text.y = element_text(size = 8), axis.title.x = element_text(size = 9), axis.title.y = element_text(size = 9), axis.line = element_line(color = «black»))
jpeg(«histograma_ERel.jpeg», width = 800, height = 600, units = «px», res = 300)
print(hist_plot6)
dev.off()
hist_plot6

Estimación puntual y por intervalo de la dispersión en variables en escala nominal

Razón de variación de Freeman

Razón de variación de Wilcox

Razón de variación universal de Moral

Desviación estándar desde la moda de Kvalseth

Índice de variación cualitativa de Gibbs y Poston

Entropía relativa de Shannon

Método

Resultados

Discusión

Conclusiones

APÉNDICES

José Moral de la Rubia

Deja un comentario Cancelar la respuesta

Nosotros

Envíos

Contacto

Suscríbase Gratis a la Revista

Razón de variación de Freeman

Razón de variación de Wilcox

Razón de variación universal de Moral

Desviación estándar desde la moda de Kvalseth

Índice de variación cualitativa de Gibbs y Poston

Entropía relativa de Shannon

Método

Resultados

Discusión

Conclusiones

APÉNDICES

Autor(es)

José Moral de la Rubia

Artículos relacionados:

Comentarios:

Deja un comentario Cancelar la respuesta

Nosotros

Envíos

Contacto

Suscríbase Gratis a la Revista